This page introduces our paper in a graphical manner. The main goal is to explain the positioning and the content of the paper in an efficient way.

Fault tolerance

Fault Tolerance is a property of systems to maintain their functionlity even when its components crash. For neural networks, this means that the output is preserved even when some neurons crash .

Picture is taken from https://towardsdatascience.com/coding-neural-network-dropout-3095632d25ce

---

Picture is taken from https://medium.com/the-spike/yes-the-brain-is-a-computer-11f630cad736

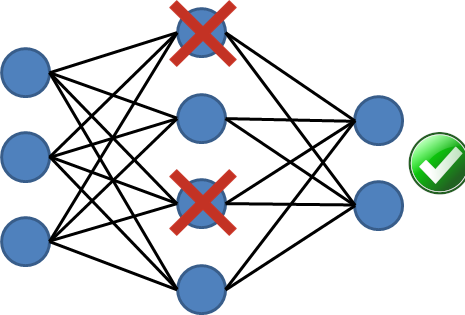
Fault tolerance in biological brains

Biological systems are known to be fault-tolerant . Neurons are unreliable, and, therefore, any single neuron cannot be crucial to the computation.

---

Fault tolerance in neuromorphic hardware

Neuromorphic hardware is an emergent computing paradigm . It promises to speed up neural network computations drastically. However, the hardware is faulty, and thus neurons crash randomly.

Picture is taken from https://www.researchgate.net/figure/Comparison-between-Brains-Computing-System-with-Conventional-Von-Neumann-Computing_fig1_316727654

---

Picture is taken from http://virgipla.wixsite.com/travellers/single-post/2017/03/07/111-Timeline-of-the-ancient-Greece

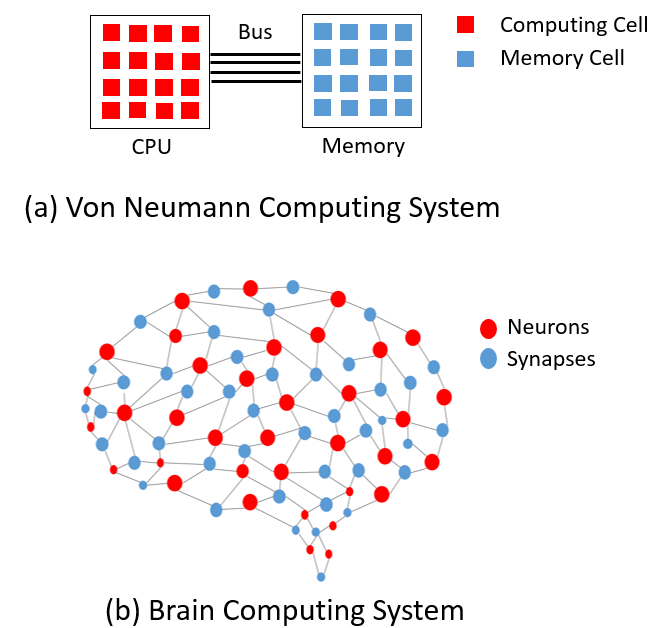
Research on fault tolerance

The problem of fault tolerance in neural networks consists of defending the performance of the network against random crashes of individual neurons. The problem was well-studied in the 90s for small networks . However, advances in neuromorphic hardware ask for research in that direction for deep networks.

---

Definitions

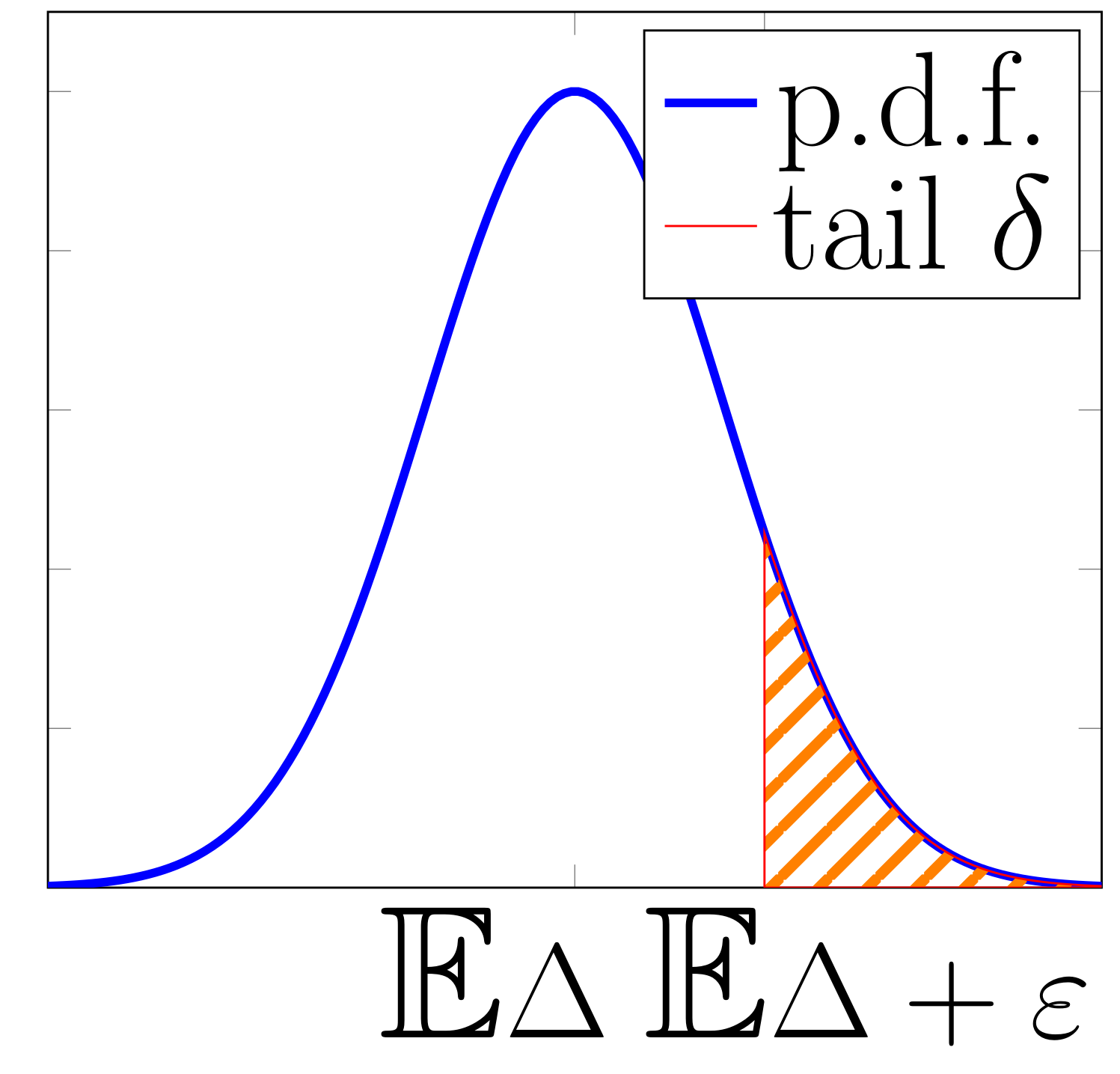
We quantify fault tolerance of a neural network as the error in the output: $$\Delta=\hat{y}-y$$ where $$\hat{y}$$ is the output of the network with crashed neurons, and $$y$$ is the original (correct) output. Our goal is to guarantee that the error $$\Delta$$ does not exceed $$\varepsilon$$ with a high probability $$1-\delta$$.

---

Picture is taken from https://en.wikipedia.org/wiki/Regularization_(mathematics)

Fault Tolerance and Dropout

Our problem is mathematically similar to the theoretical study of Dropout . In fact, Dropout was invented in the context of Fault Tolerance research . However, we are interested in the average error in the output $$\mathbb{E}\Delta$$. In contrast, Dropout is a regularization technique, and, thus, theoretical studies of it are concerned about generalization properties. Thus, these research directions are related, but fundamentally different.

---

Fault Tolerance and Adversarial Examples

Our problem is also related to the phenomenon of Adversarial Examples . Indeed, if we consider faults in the input, then fault tolerance is concerned about the classification outcome under the average perturbation $$\mathbb E_{\delta x}y(x+\delta x)$$. In contrast, Adversarial Examples are the worst-case perturbations $$ \max_{\delta x}Loss(y(x+\delta x)) $$. Thus, the problem we consider is related to adversarial examples, but, again, quite different from it.

Picture is taken from https://medium.com/@ml.at.berkeley/tricking-neural-networks-create-your-own-adversarial-examples-a61eb7620fd8

---

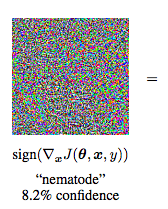
Main contribution

We derive a bound on $$\mathbb{E}\Delta$$ and Var$$\Delta$$ in the case if number of neurons $$n\to\infty$$, and if the network follows the Continuous Limit : nearby neurons compute similar functionsThe figure shows activations of neurons at one layer as the width increases. The bound uses a Taylor expansion. The main technical difficulty is to bound the remainder, which we successfully do using our assumptions. The bound is then analyzed qualitatively, and quantitatively in our experiments. It is then used to give a probabilistic guarantee on fault tolerance, giving a solution to the our problem. We show that our bound is the tight asymptotically, up to a constant factor.In the Section 4 of the paper, paragraph "The best and the worst fault tolerance" – the best variance is O(p/n), and our bound from Theorem 1 is like this as well

→See the full paper on OpenReview